Bölüm 7 Normal Dağılım ve Diğer Dağılımlar
Bu bölümde normal dağılım üzerinde durulmuş poisson ve binom dağılımı ise tanıtılmıştır.
7.1 Normal Dağılım
Normal dağılım, sürekli değişkelerin dağılımıdır (Sümbüloğlu ve Sümbüloğlu, 2012). Doğadaki birçok olayın gerçekleşmesiyle de uyum içerisindedir. Rastlantısal olarak gerçekleşen pek çok olayın dağılımı normal dağılıma uyma eğilimindedir (Arıcı, 1997). Örneğin, güvercin yumurtalarının çaplarını ölçecek olsak çok küçük ve çok büyük olanların sayıları daha az, orta büyüklükte olan yumurtaların ise daha fazla olduğunu gözleyebiliriz. Benzer şekilde toplumdan rassal olarak seçilecek 1000 bireye zekâ testi uygulansa alt ve üst gruptakiler daha az, orta gruptakiler ise daha fazla olacaktır. İnsanların psikolojik özelliklerinin de normal dağıldığı varsayılmaktadır (Baykul, 2015). Buradan hareketle psikolojide ölçtüğümüz birçok değişkenin normal dağılıma uyum göstereceği söylenebilir.
Ölçtüğümüz değişkenin normal dağılıma uyum göstermesi için en önemli koşul örneklemin yansız seçilmesidir. Yansızlığın sağlanabilmesi için de örneklem basit tesadüfi örneklemeyle seçilebilir (Baykul ve Güzeller, 2013). Örneklem büyüklüğü 30’un üzerinde ise örneklem büyüklüğü arttıkça dağılım normal dağılıma yaklaşır (Büyüköztürk vd., 2020). Burada evrenin normal dağılım göstermesi gerektiği unutulmamalıdır. Normal dağılım grafiği Şekil 13’de sunulmuştur.

Şekil 13 incelendiğinde ortalamanın \(\overline{X}\), standart sapmanın ise \({S_x}\) ile gösterildiği görülmektedir. Ortalama 0, standart sapması 1 ise bu tür normal dağılıma standart normal dağılım ya da birim normal dağılım denilmektedir (Büyüköztürk vd., 2020). Ancak tüm normal dağılımlar bu şekilde olmak zorunda değildir. Sivri ya da basık olup normal dağılım gösteren veri setleri de olabilir (Baykul, 2015). Şekil 14’te aynı ortalamaya ancak farklı standart sapmalara sahip normal dağılımlar örneklendirilmiştir.

Şekil 14 incelendiğinde ortalaması 0 olan ancak farklı standart sapmalara (dolayısıyla varyanslara) sahip dağılımlar görülmektedir. Standart sapma büyüdükçe dağılım basıklaşırken standart sapma küçüldükçe dağılım sivri hale gelmektedir (Baykul ve Güzeller, 2013). Bunu daha iyi anlamak için linkteki online araç incelenebilir (DESMOS). Ortalamanın değişmesi grafiğin x-ekseninde sağa ya da sola doğru ötelenmesine neden olurken standart sapmanın değişmesi eğrinin basık olmasına ya da sivrileşmesine neden olur (Baykul, 2015). Dağılımın kuyrukları asimptotik olup x ekseni ile kesişmez ancak gittikçe x eksenine yaklaşır (Salkind, 2011/2015).
Normal dağılım eğrisinin bazı özellikleri vardır (Sümbüloğlu ve Sümbüloğlu, 2012):
- Dağılım ortalamaya göre simetriktir (tam ortada ayna olduğunu düşünün, aynanın oluşturduğu yansıma gibi). Eğrinin altında kalan alanın %50’si ortalamanın sağında, %50’si de ortalamanın solundadır.
- Eğriyle x-ekseni arasındaki toplam alan bir birim karedir.
- Normal dağılım eğrisinin altında kalan alan olasılık belirtir.
- Normal dağılımda mod, medyan ve aritmetik ortalama birbirine eşittir. Mod, tek ve ortadadır.
- Normal dağılım eğrisinin altında kalan alan standart sapmaya göre belirlenebilir. Şekil 15’te normal dağılım altında kalan alanın nasıl bölündüğü sunulmuştur.
- Dağılım çan eğrisi şeklindedir. Ancak her çan eğrisi biçimindeki dağılım normal dağılım değildir.
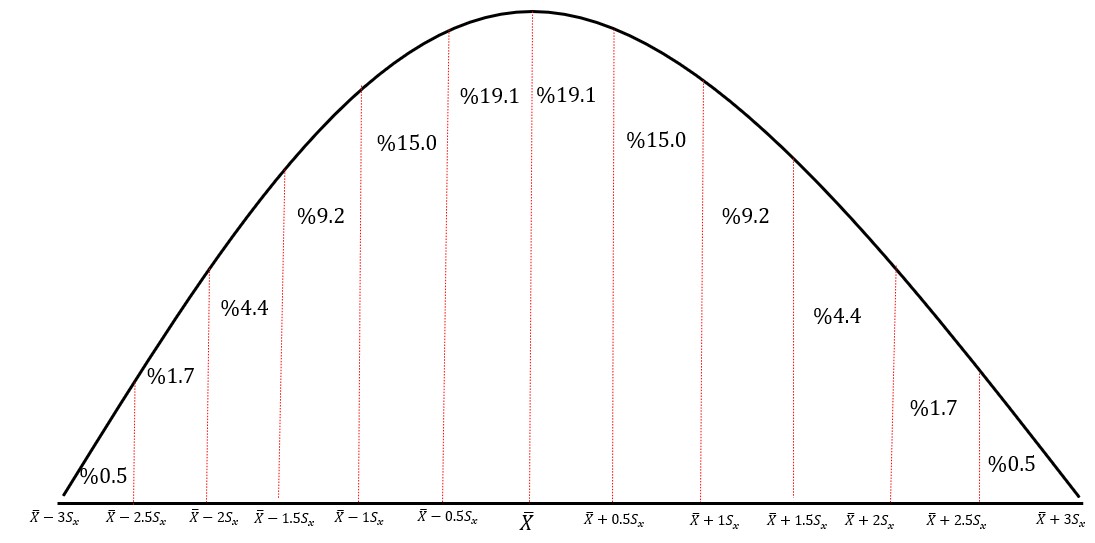
Normal dağılımın bu özelliği, öğrencilerin puanları hakkında yorum yaparken kullanılabilir. Ayrıca ölçmenin standart hatasını belirledikten sonra da öğrenci puanlarının ihtimaller dahilinde hangi aralıklarda yer aldığı yorumu yapılabilmektedir. Buradaki kritik nokta hata puanlarının normal dağıldığı varsayımıdır. Benzer şekilde öğrenci puanlarının dağılımı normal dağılıma uyum gösteriyorsa bu durumda ortalama ve standart sapma bilgisini kullanarak bir öğrencinin hangi yüzdelik dilimde yer aldığı yorumu yapılabilir (Can, 2017).
Örneğin; Serap öğretmenin 100 öğrencinin katılımıyla gerçekleştirdiği kimya sınavı sonrası puanların normal dağıldığını gözlemiştir. Sınavın ortalaması 40 standart sapması ise 8’dir. Buna göre Serap hocanın sınavından 60 puan alan Eymen, öğrencilerin yüzde kaçından daha yüksek puan almıştır?
Ortalama 40, standart sapma 8 olduğu ve puanlar normal dağılım gösterdiğinden puanlar şu şekilde dağılacaktır.
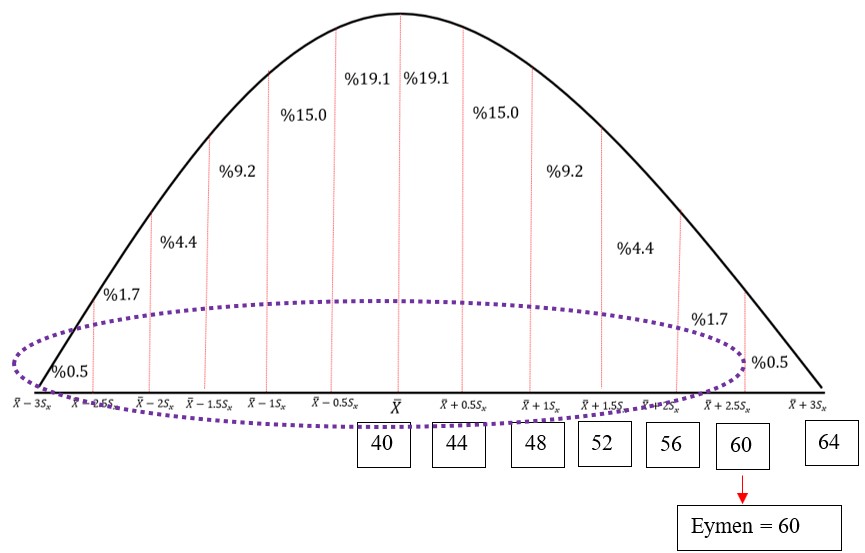
Puanlar belirtilen aralıklarda yer alacaktır. Eymen 60 puan almıştı. Puanı grubun ortalamasının 2 standart sapma üzerinde olup mor ile işaretli yüzdelerin toplamından daha yüksek bir puana sahip olduğu söylenebilir. Eğer Eymen ortalama kadar puan almış olsaydı grubun %50’sinden daha yüksek puan almış olacaktı. %50’nin üzerine %34,13 ve %13,60’ı ekleyerek Eymen’in grubun yüzde kaçından yüksek puan aldığı bulunabilir. Buna göre Eymen’in grubun %50 + %34,13 + %13,60 = %97,73’ünden daha yüksek puan aldığı söylenebilir. Dağılımların ortalama ve standart sapması değişse de standart sapma değerleri arasında kalan alanların yüzdeleri değişmez (Arıcı, 1997). Örneğin normal dağılımlarda her zaman -2 ile -1 standart sapma aralığı gruptaki bireylerin %13,6’sını kapsar. Dağılımın normal olduğunu düşünürsek puanların %99,7’sinin -3 ile +3 standart sapma aralığında olduğunu belirtebiliriz (Atılgan, 2017).
7.2 Dağılımın Normal Olup Olmadığını İncelenmesi
Verilerin normal dağılım gösterip göstermediğini incelemek için birkaç yöntem bulunmaktadır. Ancak normallik, tek değişkenli ve çok değişkenli normallik olmak üzere iki başlık altında incelenebilir. Şekil 16’te normal dağılımı belirleme yolları özetlenmiştir. Ders kapsamında tek değişkenli istatistikler incelendiği için çok değişkenli normallikten bahsedilmeyecektir. Tek değişkenli normal dağılım ise tek değişkenin normal dağılım gösterip göstermediğinin incelenmesidir. Örneğin matematik testinden alınan puanların normal dağılım gösterip göstermediğinin incelenmesi tek değişkenli normalliğin incelenmesidir. Çünkü matematik testinden alınan puanlar ifadesindeki tek değişken matematik puanlarıdır.
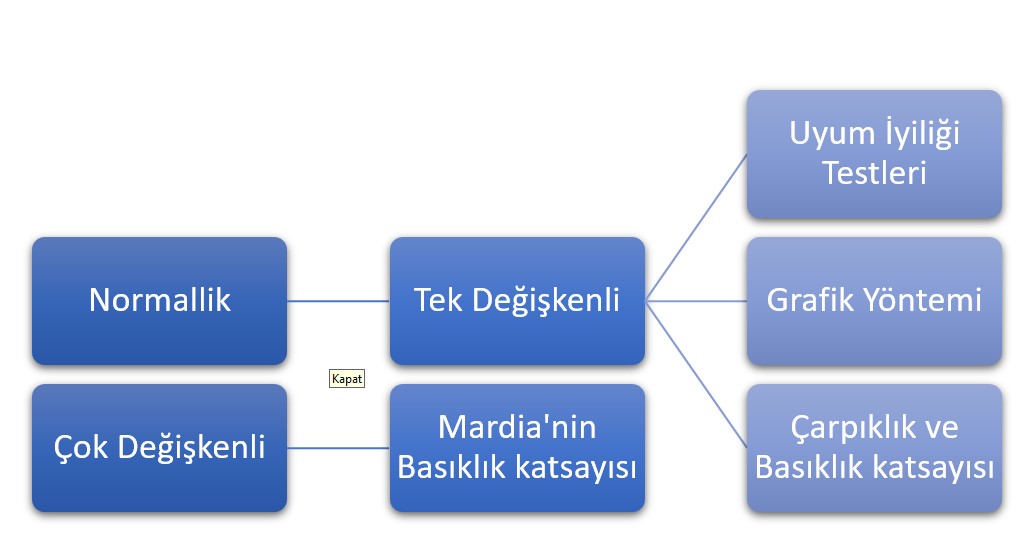
Şekil 16’te sunulan yöntemlerin haricinde de birçok yöntem bulunmaktadır. Ancak bu ders kapsamında yeterli olması ve eğitim alanında en çok kullanan yöntemler olması nedeniyle belirtilen yöntemler üzerinde durulacaktır.
7.2.1 Uyum iyiliği testleri
Bir değişkenin normal dağılım gösterip göstermediğini incelemek için tek örneklem Kolmogorov-Smirnov testi ya da Shapiro-Wilk testi gerçekleştirilebilir. Örneklem büyüklüğünün 50’den küçük olması durumunda Shapiro-Wilk, 50’den büyük olması durumunda ise Kolmogorov Smirnov testinin kullanılması önerilmektedir (Büyüköztürk, 2019). Ancak bu testler büyük örneklemlerde (örneğin 1000) normal dağılım gösteren veri setlerinde bile istatistiksel olarak anlamlı çıkma eğilimindedir (Pallant, 2016). Yani normal dağılım gösteren veri setlerinde dahi normal dağılım göstermiyor şeklinde sonuç vermektedir. Çünkü yöntemlerin kullandığı istatistik ki-kare istaistiğine dayanmakta olup örneklem büyüklüğünden etkilenmektedir (Pituch ve Stevens, 2016).
7.2.2 Grafik Yöntemi
Dağılımın grafiği çizilerek yorum yapılmasını gerektirir. Histogram ve normal dağılım eğrisinin üst üste çizilmesiyle incelenebilir (Pituch ve Stevens, 2016). Şekil 17’de Türkçe testinden elde edilen puan dağılımı sunulmuştur.
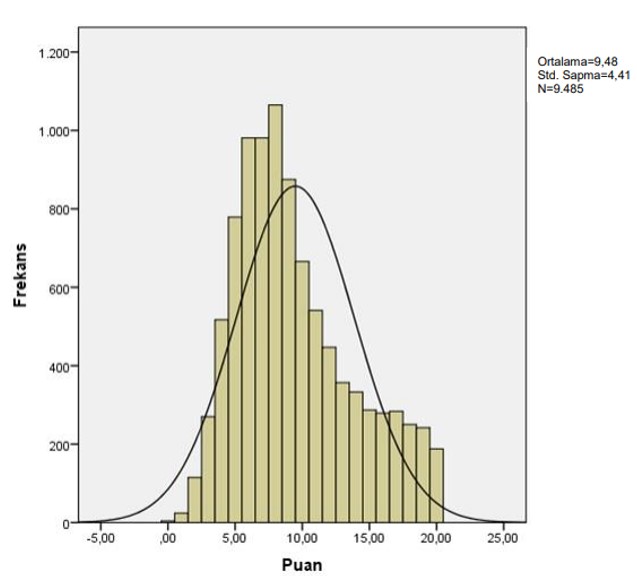
Şekil 17 incelendiğinde dağılımın bir miktar sağa çarpık olduğu söylenebilir. Ancak sağa çarpık olmasına neden olan frekansı yüksek değerler orta noktadan çok fazla uzaklaşmamıştır. Bu nedenle bu dağılımın normallikten çok fazla sapmadığı söylenebilir.
7.2.3 Çarpıklık ve Basıklık Katsayısı
Çapıklık bir dağılımın orantısızlığının ve asimetrikliğinin bir ölçüsü iken basıklık bir dağılımın sivriliğinin bir ölçüsüdür (Salkind, 2011/2015). Normal dağılım gösteren bir verinin basıklık ve çarpıklık katsayısı 0’dır (Büyüköztürk vd., 2020). Ancak bu durum pratikte pek mümkün olmamaktadır. Çarpıklık katsayıları normalden (yani 0’dan) uzaklaştıkça veri setinin dağılımı da normalden uzaklaşarak sağa ya da sola çarpık hale gelmektedir (Atılgan, 2017). Bu nedenle çarpıklık katsayısının [-1, +1] aralığında yer alması durumunda verinin normallikten aşırı sapma göstermediği söylenebilir (Büyüköztürk, 2019). Bu nedenle çarpıklık katsayısının [-1, +1] aralığında olması normalliğin sağlandığının bir göstergesi olarak değerlendirilebilir. Ancak grafik yöntemiyle birlikte kullanılması önerilmektedir (Tabachnick ve Fidell, 2019). Negatif çarpıklık değeri sola çarpık dağılıma, pozitif çarpıklık değeri sağa çarpık dağılıma işaret edebilir (Can, 2017).
7.2.4 Mod, Medyan ve Aritmetik Ortalama
Bir dağılımda; mod (tepe değer), ortanca ve aritmetik ortalamadan küçük olduğunda grafiğin solunda verilerin yığıldığı gözlenmektedir. Bu durumda Mod < Medyan < Aritmetik Ortalama olmaktadır. Bu dağılıma sağa çarpık dağılım denilmektedir (Uyar, 2019). Sağa çarpık dağılımda mod, aritmetik ortalamadan küçük olduğu için aritmetik ortalamanın altında puan alan daha fazla bireyin olduğu söylenebilir. Sola çarpık dağılımda ise Aritmetik ortalama < Medyan < Mod olmaktadır (Arıcı, 1997). Mod, aritmetik ortalamadan büyük olduğunda gruptaki bireylerin çoğu, aritmetik ortalamadan daha yüksek puana sahiptir. Şekil 18’te sağa ve sola çarpık dağılımın görseli sırasıyla sunulmuştur.
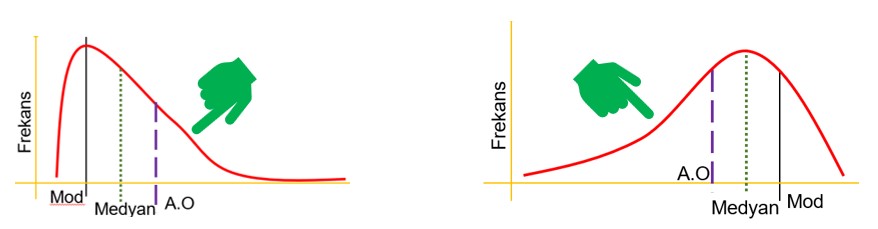
Şekil 18’te ilk dağılım sağa çarpık ikinci dağılım ise sola çarpıktır. Grafikteki el işaretlerini inceleyiniz. Normal dağılım grafiğine ne taraftan bastırılmışsa çarpıklık o şekilde adlandırılmaktadır. Örneğin sağa çarpık grafikte el sağ tarafta bulunmaktadır. Benzer şekilde sola çarpık grafikte de el sol taraftadır. Bu bir analoji olarak akılda kalmayı artırmak amacıyla kullanılmıştır.
7.3 Diğer Dağılımlar
Teorik dağılımlardan yararlanarak herhangi bir olayın beklenen olası sonuçları değerlendirilebilir (Sümbüloğlu ve Sümbüloğlu, 2012). Bir olayın olabilme ihtimalini kestirmek ise oldukça önemlidir. Çok sayıda teorik dağılım bulunmaktadır. Normal dağılım da bunlardan biridir. İnsanın psikolojik özellikleri normal dağılım gösterdiği için normal dağılımla ilgili daha fazla ayrıntıya yer verilmiştir. Ancak normal dağılım haricinde Poisson ve binomiyal dağılımla ilgili de bilgi verilmesi dağılımlar hakkında genel bilgiye sahip olunmasını sağlayacaktır.
Bir dağılımın normal olabilmesi için öncelikle ölçülen özelliğin sürekli olması gerekmektedir. Ancak ölçülen özelliğin sürekli olmadığı durumlarda nasıl dağılımlar oluşmaktadır? İşte ölçülen özellik sürekli değilse bu durumda poisson ve binomiyal dağılım kullanılabilir. Örneğin binomiyal dağılım sayımla belirlenen kesikli değişkenlerin dağılımıdır. Örneğin binomiyal dağılım yardımıyla uygulanan bir ilaç tedavisinin hastalardan kaçının hangi olasılıkla iyileşmesini sağlayacağını tahmin edebiliriz (Sümbüloğlu ve Sümbüloğlu, 2012). Poisson dağılımı da binomiyal dağılımda olduğu gibi kesikli değişkenlerin dağılımıdır. Ancak toplam olay sayısı büyüdükçe (n) binomiyal dağılımla hesaplama zorlaştığından Poisson dağılımı kullanılmaktadır. Poisson dağılımı daha basit bir hesaplamaya sahiptir.