Bölüm 4 Betimsel İstatistikler: Merkezi Eğilim (Yığılma) Ölçüleri
Veri setini betimlemek daha önce de bahsettiğimiz gibi grubun daha iyi anlaşılmasını ve verilerin daha iyi yorumlanmasını sağlar. Örneğin; başarı puanları bilinen bir sınıfta grubu daha iyi tanımak ve eğitimi bireyselleştirmek için merkezi eğilim ölçüleri kullanılabilir. Merkezi eğilim (merkeze yığılma) ölçüleri, bir veri kümesinde ölçümlerin etrafında toplandığı veya etrafında yığılma eğilimi gösterdiği değerlerdir (Baykul, 2015). Bu değerlerin, tüm puanları/sayıları temsil ettiği söylenebilir. Bu değerler, veri kümesini betimlemektedir (Baykul ve Güzeller, 2013; Salkind, 2011/2015). Puanlar dokuzuncu sınıf öğrencilerinin matematik testinden gelebileceği gibi Psikolojik İyi Oluş ölçeğinden de gelebilir. Yıllara göre rehberlik servisine başvuran öğrenci sayısı olabilir.
Bu bölümde merkezi eğilim ölçüleri olan mod (tepe değer), medyan (ortanca) ve aritmetik ortalama üzerinde durulacaktır. Bu ölçülerin her biri puan dağılımı ile ilgili farklı türde bilgiler sunmaktadır (Salkind, 2011/2015).
4.1 Mod (Tepe Değer)
Bir puan dağılımı içinde en çok tekrar eden puan mod (tepe değer) olarak adlandırılır (Büyüköztürk vd., 2020). Frekansı (sıklığı) en yüksek olan puan, tepe değerdir (moddur). Mod değerinin en genel ve en az hassas olduğu belirtilebilir (Atılgan, 2017). Formülü yoktur (Salkind, 2011/2015). Mod, üç farklı şekilde hesaplanabilir:
- Ham puan frekans tablosuyla
- Grafik yoluyla
- Gruplanmış puan tablosundan
Bir veri setinde birden fazla mod olabilir. Eğer iki mod varsa (yani iki değerin frekansı en yüksek ve birbirine eşitse) bu veri setinin çift modlu olduğu söylenebilir (Uyar, 2019). Örneğin eğitim durumuna göre lisans ve ortaöğretim mezunu frekansı 30 ve bu değer en yüksek olsun. Bu durumda dağılım çift modlu olacaktır. Burada mod, lisans ve ortaöğretim düzeyleridir. Eğer ikiden fazla mod varsa bu durumda dağılım çok modlu olarak isimlendirilir ve mod kullanmak doğru değildir (Baykul ve Güzeller, 2013). Mod, çok modlu veri setlerine uygun bir ölçü olmamaktadır (Sümbüloğlu ve Sümbüloğlu, 2012). Ayrıca veri setinde tüm frekanslar eşitse mod yoktur (Atılgan, 2017). Örneğin herkes 8 puan aldıysa mod yoktur demelisiniz.
4.1.1 Ham puan frekansıyla tepe değeri bulma
Ham puan frekansıyla tepe değeri elde etmek için ham puanlardan kaç tane olduğu sayılır. Örneğin en düşük 0, en yüksek 5 puan alınabilen bir testten 40 öğrencinin aldığı puanlar şöyle olsun:
1, 1, 0, 1, 2, 0, 3, 0, 4, 2, 4, 3, 4, 2, 5, 5, 1, 2, 0, 0, 0, 5, 1, 3, 1, 5, 1, 1, 0, 2, 5, 0, 4, 0, 0, 4, 2, 0, 1, 5
Buna göre bu ham puan dağılımının modu yani tepe değeri kaçtır? Bu değerlerle oluşturulan frekans tablosu Tablo 8’de sunulmuştur.
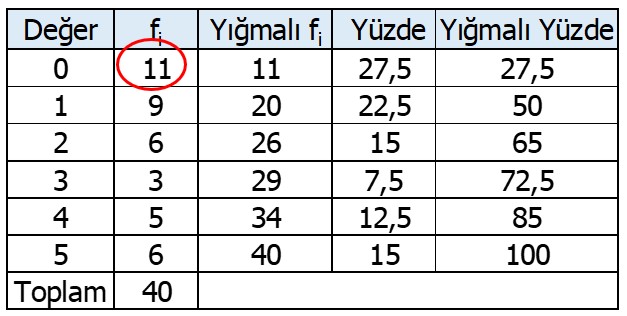
Tablo 8 incelendiğinde 0 puan alan 11 kişi, 1 puan alan 9 kişi, 2 puan alan 6 kişi, 3 puan alan 3 kişi, 4 puan alan 5 kişi ve 5 puan alan 6 kişi olduğu görülmektedir. Tepe değer bir veri setinde en çok tekrar eden değer demekti. Buna göre bu veri setinde en çok tekrar eden, frekansı en yüksek olan değer 0’dır. Bu durumda veri setinin modu 0’dır.
4.1.2 Grafik yoluyla tepe değeri bulma
Herhangi bir frekans grafiği yardımıyla dağılımın tepe değeri bulunabilir. Burada dikkat edilmesi gereken nokta, tepe değer y-eksenindeki değer DEĞİLDİR. Tepe değer, x-eksenindeki değerdir.
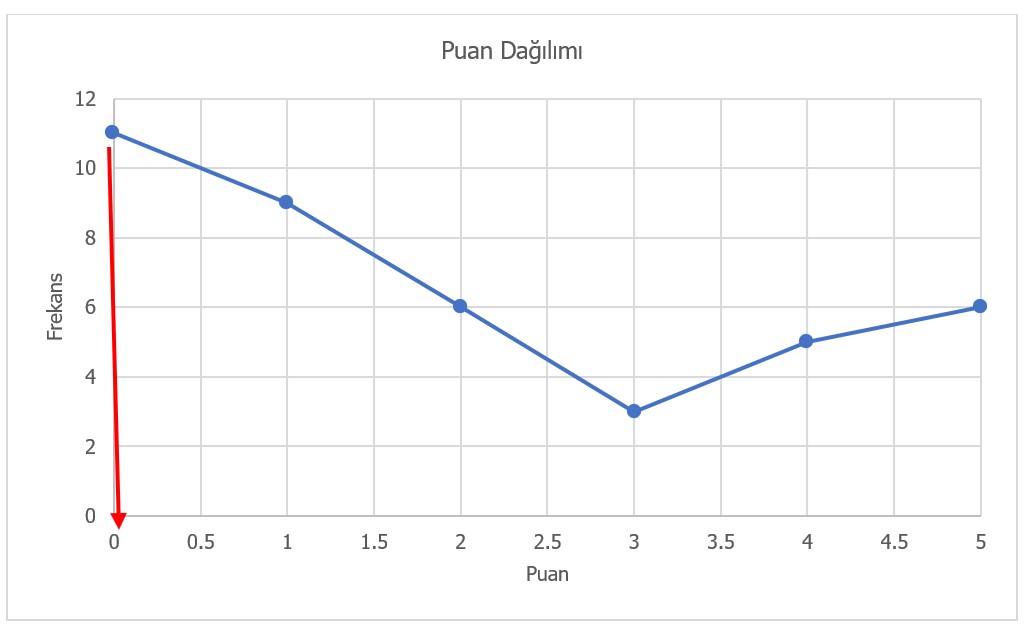
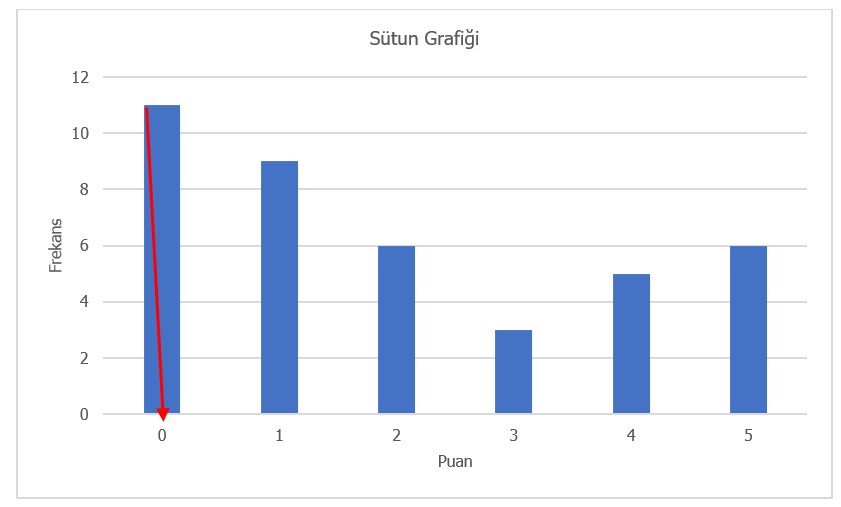
Şekil 10 ve Şekil 11’de verilen grafikler yardımıyla mod elde edilebilir. Bu iki grafik de Tablo 8’de sunulan veri setinin grafiğidir. Grafik incelendiğinde frekansı en yüksek olan puanın 0 olduğu görülmektedir. Grafikte mod bulunurken en sık yapılan hata, frekans değerinin mod olduğunu düşünmektir. Örneğin Şekil 10 ve Şekil 11’de frekans değeri olan 11, mod olarak düşünülmemelidir. Mod puan aralığından bir değer olmalıdır.
4.1.3 Gruplanmış veri tablosundan tepe değeri bulma
Gruplanmış verilerde mod bulunurken öncelikle frekansı en yüksek grup incelenir. Daha sonra bu en yüksek frekansa sahip grubun orta noktası bulunur (Uyar, 2019). Bulunan bu orta nokta moddur. Daha önce Tablo 6’da sunulan verilere, grup orta noktası da eklenerek Tablo 9 yeniden sunulmuştur.

Tablo 9’da sunulan gruplanmış verilerde frekansı en büyük olan grup, 39-43 puan aralığıdır. Bu aralığın orta noktası ise 41’dir
(\(\frac{38,5+43,5}{2}\)). Buna göre veri setinin modu 41’dir.
4.2 Medyan (Ortanca)
Bir veri seti sıralandığında orta noktasındaki veriye medyan denir (Uyar, 2019). Diğer bir deyişle medyanın sağında ve solunda eşit sayıda veri vardır (Turgut ve Baykul, 2012). Puanların %50’si medyanın altındadır dolayısıyla 50. yüzdelik olarak isimlendirilir (Büyüköztürk vd., 2020). Medyan veri sayısından etkilenmektedir (Atılgan, 2017). Ancak uç değerlerden etkilenmemektedir (Atılgan, 2017). Örneğin 21 kişilik veri setinde 11. sıradaki veri medyandır. Bu veri setine 2 kişi daha eklenirse medyan 12. değere karşılık gelecektir. Ancak 21 kişilik veri setinde uç değerler bulunsa da medyan bundan etkilenmeyecektir.
Medyan bulunurken öncelikle veri setindeki eleman sayısı, diğer bir değişle veri sayısına bakılır. Eğer veri sayısı tek ise (n olsun) medyan \(\frac{n+1}{2}\) ile hesaplanır. Eğer veri sayısı çift ise bu durumda medyan \(\frac{n}{2}\) ile \(\frac{n+2}{2}\) inci sıradaki verilerin ortalamasıdır (Büyüköztürk vd., 2020).
Örneğin en düşük 0, en yüksek 5 puan alınabilen bir testten 40 öğrencinin aldığı puanlar şöyle olsun:
1, 1, 0, 1, 2, 0, 3, 0, 4, 2, 4, 3, 4, 2, 5, 5, 1, 2, 0, 0, 0, 5, 1, 3, 1, 5, 1, 1, 0, 2, 5, 0, 4, 0, 0, 4, 2, 0, 1, 5
Buna göre bu ham puan dağılımının medyanı yani ortancası kaçtır? Bunun için öncelikle veri seti küçükten büyüğe (ya da büyükten küçüğe) doğru sıralanır. Daha sonra veri sayısı tek ise \(\frac{n+1}{2}\) inci sıraya karşılık gelen değer, çift ise \(\frac{n}{2}\) ile \(\frac{n+2}{2}\) inci sıraya karşılık gelen değerlerin ortalaması medyan olacaktır. Veri setinin küçükten büyüğe doğru sıralanmış hali Tablo 10’da sunulmuştur.
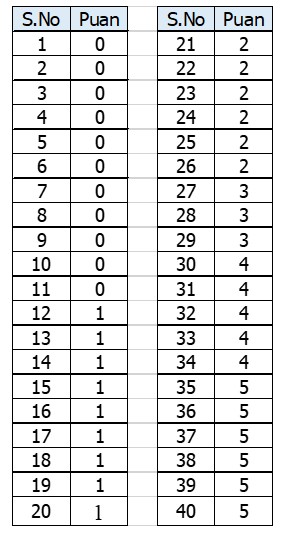
Tablo 10 incelendiğinde, veri setinde 40 kişinin olduğu görülmektedir. Bu sayı çift bir sayı olduğu için medyan \(\frac{n}{2}\) ile \(\frac{n+2}{2}\) inci sıraya karşılık gelen puanların aritmetik ortalaması olacaktır. Yani medyan, \(\frac{40}{2}\) = 20. Diğer taraftan \(\frac{40+2}{2}\) =21. sıradaki verilerin ortalaması olacaktır. Buna göre sırasıyla 20. ve 21. sıradaki verilerin 1 ve 2 olduğu görülmektedir. Bu durumda medyan \(\frac{1+2}{2}\) = 1,5 olarak karşımıza çıkar.
Veri setinde tek sayıda veri olsaydı, örneğin Tablo 10’daki veri setinde 40. puan olmayıp 39 ile bitmiş olsaydı bu durumda medyan, \(\frac{n+1}{2}\) = \(\frac{39+1}{2}\) = \(\frac{40}{2}\) = 20. sıradaki veri olacaktı. 20. sıradaki verinin ise 1 olduğu görülmektedir.
Medyan, veride uç değerler (normalden aşırı sapan değerler) olduğunda kullanılması tavsiye edilen bir ölçüdür (Büyüköztürk vd., 2020). Örneğin bir testten öğrenciler 5, 5, 10, 15, 20, 25, 100 puan almış olsunlar. Burada yer alan 100 puan uç veri durumundadır. Doğası gereği uç değerlerden etkilenmez. Böylece uç veri içeren verileri daha iyi temsil edebilir (Salkind, 2011/2015).
4.3 Aritmetik Ortalama
Merkezi eğilim ölçülerinden en çok kullanılanı, aritmetik ortalamadır (Baykul ve Güzeller, 2013). Çünkü aritmetik ortalama veri setindeki tüm veriler kullanılarak hesaplanır (Büyüköztürk vd., 2020). Ancak mod ve medyan böyle değildir.
4.3.1 Ham veride aritmetik ortalama bulma
Aritmetik ortalama, veri setindeki tüm değerlerin toplamının değer sayısına bölünmesiyle elde edilir (Baykul, 2015). \(\overline{X}\) ortalamayı, \(\Sigma\) toplamı, n değer sayısını göstermek üzere;
\[
\overline{X}=\frac{X_1+X_2+X_3+\ldots+X_n}{n}=\frac{\sum_{i=1}^{n}X_i}{n}
\]
şeklinde ifade edilebilir. Burada \(X_{1}\) birinci kişinin puanını, \(X_{2}\) ikinci kişinin puanını, …, \(X_{n}\) ise n. kişinin puanını ifade etmektedir. Denklem 1’de verilen n ise gruptaki kişi sayısını ifade etmektedir. Örneğin en düşük 0, en yüksek 5 puan alınabilen bir testten 40 öğrencinin aldığı puanlar şöyle olsun:
1, 1, 0, 1, 2, 0, 3, 0, 4, 2, 4, 3, 4, 2, 5, 5, 1, 2, 0, 0, 0, 5, 1, 3, 1, 5, 1, 1, 0, 2, 5, 0, 4, 0, 0, 4, 2, 0, 1, 5
Buna göre bu ham puan dağılımının ortalaması kaçtır?
1+ 1+ 0+ 1+ 2+ 0+ 3+ 0+ 4+ 2+ 4+ 3+ 4+ 2+ 5+ 5+ 1+ 2+ 0+ 0+ 0+ 5+ 1+ 3+ 1+ 5+ 1+ 1+ 0+ 2+ 5+ 0+ 4+ 0+ 0+ 4+ 2+ 0+ 1+ 5 = 80 (değerleri toplayınız).
40 kişilik veri olduğu için 80/40 = 2 grubun ortalamasıdır. \(\overline{X}\) (X bar diye okunur) = 2’dir.
4.3.2 Frekans tablosundan ortalama hesaplama
Frekans tablosu hangi puandan kaç tane olduğunu göstermektedir. Toplam puanı elde etmek için her bir puan frekans ile çarpılıp tümü toplanır. Daha sonra da frekanslar toplamına bölünürse yine aritmetik ortalama elde edilir (Büyüköztürk vd., 2020). Formülü Denklem 2’de verilmiştir. f frekansı (sıklığı) göstermek üzere;
\[
\bar{X}=\frac{\sum_{j=1}^{K}{f_jX}_j}{n}
\]
Burada \(f_{j}\), frekans tablosundaki j. ölçümün frekansı, \(X_{j}\) ise j. ölçümün puanı, n ise frekanslar toplamıdır. Örneğin Tablo 11’de sunulan frekans tablosundan grubun ortalamasını hesaplayalım.
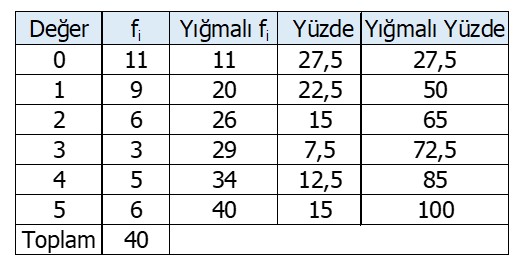
Tablo 11 incelendiğinde 0 puanından 11, 1 puanından 9, 2 puanından 6, 3 puanından 3, 4 puanından 5 ve 5 puanından 6 tane bulunduğu söylenebilir. Bu durumda aritmetik ortalama;
\[
\frac{0.11+1.9+2.6+3.3+4.5+5.6}{11+9+6+3+5+6}=\frac{9+12+9+20+30}{40}=\frac{80}{40}=2
\]
olarak elde edilir.
Aritmetik ortalama, veri setindeki tüm verileri kullanarak hesaplandığı için güçlü bir istatistiktir (Turgut ve Baykul, 2012). Ancak veri setinin dağılımı normal ya da normale yakın olduğunda kullanmak daha doğrudur (Büyüköztürk vd., 2020). Ayrıca ölçülen değişken en az eşit aralık ölçeğinde olması gerekir. Örneğin illerin plaka kodlarının ortalamasını hesaplamanın bir anlamı olmayacaktır. Ya da kızların 1 erkeklerin 2 ile kodlandığını düşünelim. Bu sayıların ortalamasını almak bir şey ifade etmeyecektir.
Aritmetik ortalama uç değerlerden de etkilenen bir istatistiktir (Güler, 2019). Örneğin 35 kişilik bir sınıfta 33 kişi 65 ve üzerinde puan almışken 2 kişi 10 puan almışsa, bu 2 kişi uç değer olarak nitelendirilebilir. Benzer şekilde 33 kişinin 50’nin altında puan aldığı bir sınavda 2 kişi 95 almışsa yine bu iki kişi uç değer olarak nitelendirilebilir. Eğer veride uç değerler varsa aritmetik ortalama dağılımı iyi temsil etmeyecektir (Uyar, 2019). Örneğin 10 öğrencinizin dokuzunun ailesinin geliri 6000 liraya çok yakın ancak birinin ailesinin geliri 90000 lira olsun. Bu durumda 90000 liralık gelir ortalamayı yüksek gösterecektir. Ancak tüm ailelerin gelirleri bu düzeyde olmayacaktır. Bu durumda aritmetik ortalama kullanmak doğru değildir. Aritmetik ortalama uç değerlerin varlığında grubu o özellik açısından ya olduğundan düşük ya da yüksek gösterecektir (Uyar, 2019). Grup hakkında doğru bilgi vermeyecektir. Bu gibi durumlarda aritmetik ortalama yerine medyan kullanılması gerekmektedir (Büyüköztürk vd., 2020). Ayrıca eğer veriler sıralama ölçeğinde elde edilmişse aritmetik ortalama hesaplanamayacağı için yine medyan kullanmak gerekir (Baykul ve Güzeller, 2013). Veriler sınıflama ölçeğinde ise bu durumda da mod’un kullanılması gerekir. Ayrıca ortalamanın ortancadan, ortancanın moddan daha hassas bir ölçü olduğunu belirtebilir (Turgut ve Baykul, 2012).
4.3.3 Mod, Medyan ve Aritmetik Ortalamanın Birbirine Göre Durumları
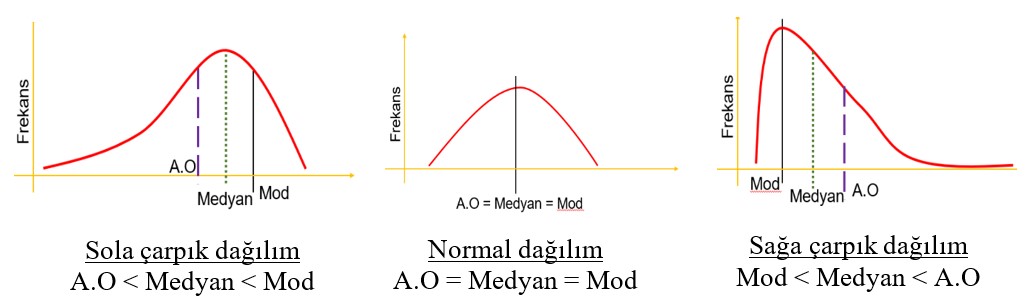
Mod, medyan ve aritmetik ortalamanın birbirine göre durumları, veri setinin dağılımı hakkında bilgi vermektedir (Atılgan, 2017):
- Aritmetik ortalama = Medyan = Mod ise veri normal dağılıyor demektir (çan eğrisi).
- A.O < Medyan < Mod ise veri sola çarpık (kayışlı) demektir.
- Mod < Medyan < A.O ise veri sağa çarpık (kayışlı) demektir.
Veri normal dağılıyorsa, öğrencilerin yarısı ortalamanın altında, yarısı ortalamanın üzerindedir (Güler, 2019). Testin gruba normal geldiği, grubun başarısının normal olduğu söylenebilir. Veri sola çarpık dağılıyorsa, öğrencilerin çoğu ortalamanın üzerinde puan almıştır. Test gruba kolay gelmiştir ve grubun başarısının yüksek olduğu söylenebilir. Veri sağa çarpık dağılıyorsa, öğrencilerin çoğu ortalamanın altında puan almıştır. Test gruba zor gelmiştir ve grubun başarısının düşük olduğu söylenebilir (Uyar, 2019). Şekil 12’de dağılımların grafikleri verilmiştir.